对量子霍尔效应【1, 2】的探究开启了拓扑物理的大门，也催生出了凝聚态物理中丰富多彩的拓扑量子材料的研究【3, 4】。在这之后，从拓扑绝缘体【5-7】、拓扑晶体绝缘体【8】到拓扑狄拉克半金属【9-11】、拓扑外尔半金属【12-16】和拓扑nodal-line半金属【17】再到拓扑超导【18-20】，一个又一个材料体系的发现掀起了一轮又一轮的拓扑量子物态的研究热潮。 回顾过去十几年的拓扑物理研究热潮，角分辨光电子能谱（ARPES）在这一领域的研究中起到了关键作用，利用ARPES不但能识别拓扑体带的特征，如体能带反演、狄拉克点、外尔点等，也能直接探测到受拓扑保护的边界态，如狄拉克表面态、表面费米弧、鼓膜表面态和铰链态等等；另一方面，利用具有自旋分辨能力的角分辨光电子能谱(SARPES)，能够直接探究拓扑电子态在动量空间的特殊自旋织构；近年来新发展的具有时间分辨能力的角分辨光电子能谱还能探究拓扑态在时域空间的演化，如Floquet等。 我们组利用自主发展的高分辨、高统计的真空紫外激光角分辨光电子能谱系统，在拓扑量子态的研究历程中做出了许多里程碑式的工作。

　拓扑绝缘体代表一种全新的量子物态【3, 4, 7】，拥有奇异的电子态性质：它的体态是有能隙的半导体／绝缘体，表面则表现为没有能隙的金属态。由于拓扑序的保护，它的表面态穿越费米能奇数次，同时表面态具有鲁棒性，不易被破坏【21, 22】。同时它具有线性色散关系和特殊自旋织构【4】的狄拉克费米子。

我们组首先生长出了一系列高质量的Bi2(Te,Se)3拓扑绝缘体单晶样品，实现了样品体态载流子从电子型到空穴型的演变。同时利用自主研制的高分辨率真空紫外激光角分辨光电子能谱系统【23】，对典型的三维拓扑绝缘体Bi2Se3和Bi2Te3在暴露空气后的表面态电子结构进行了研究【22】。后来针对三维拓扑绝缘体材料中研究最广泛的Bi2(Te,Se)3体系，虽然已有大量的研究工作，但实验上一直很难直接观测狄拉克费米子的输运特性的问题，我们对典型的三维拓扑绝缘体Bi2(Te,Se)3体系中狄拉克费米子的动力学性质进行了系统深入的研究并取得了重要结果【24】。 同时我们利用自主研发的自旋分辨角分辨光电子能谱系统【25】，对Bi2Se3的自旋结果做了深入的研究，观察到了一种新的基于自旋和形成表面态的p轨道电子的织构【25】。

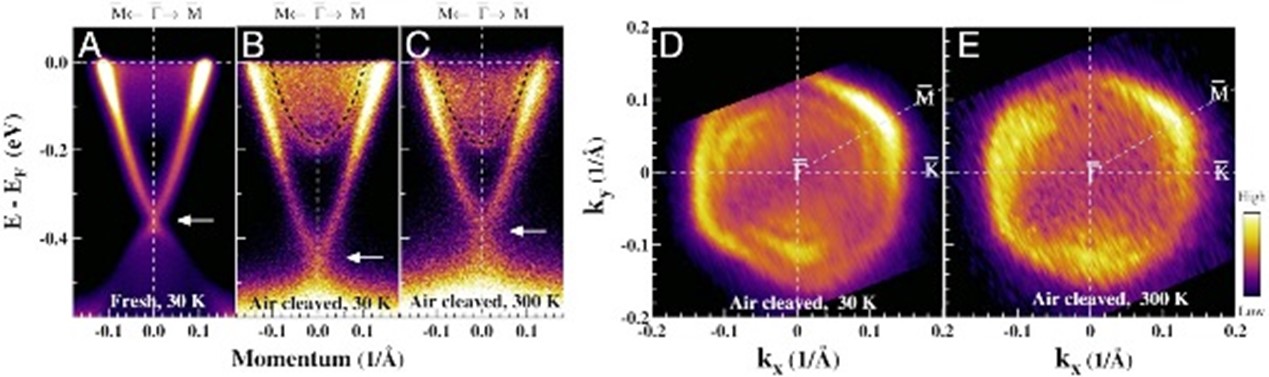
图一，空气解理的拓扑绝缘体Bi2Se3能带与费米面

图二，空气解理及暴露氮气后的拓扑绝缘体Bi2Te3的能带与费米面。图4a和b为真空解理样品的能带。图4l为理论计算七层Bi2Te3薄膜的能带

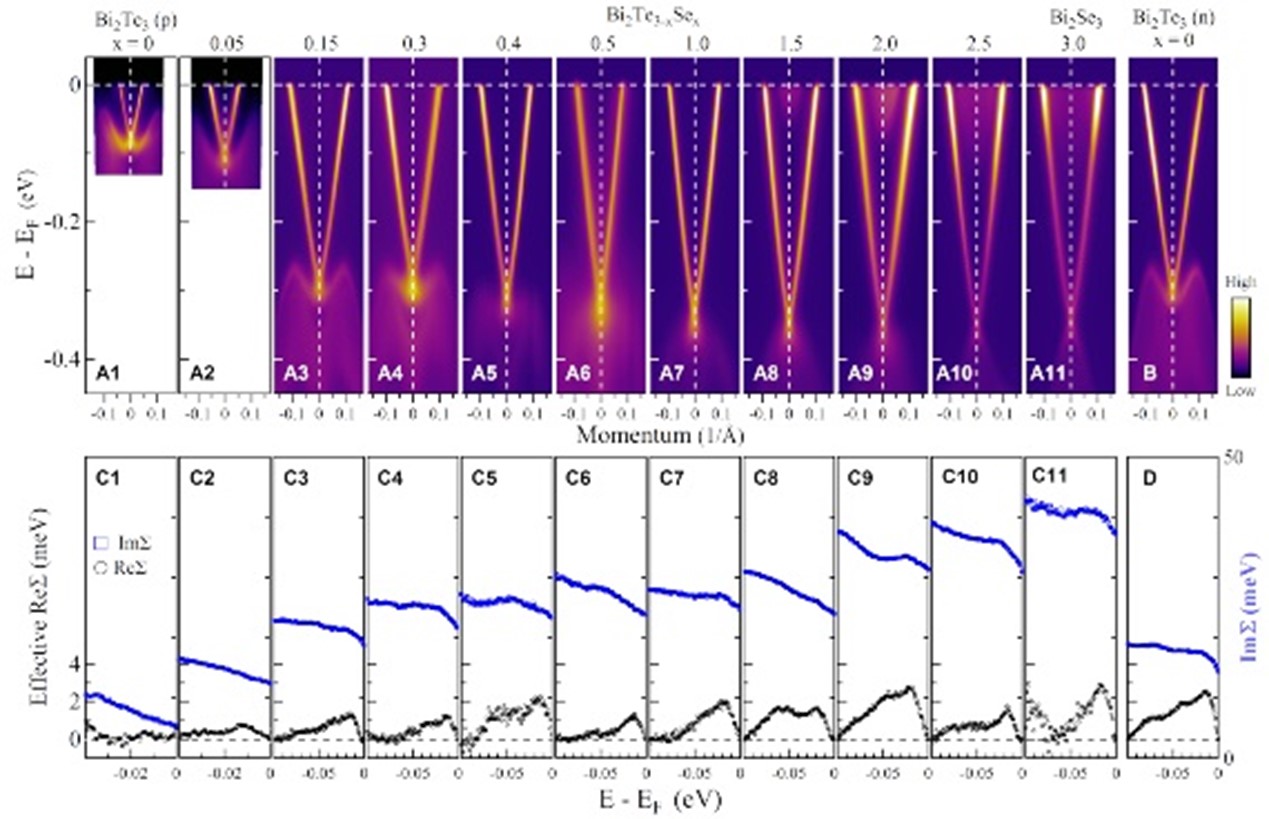
图三. 拓扑绝缘体Bi2(Te3-xSex)表面态电子结构和电子自能随组分的演变

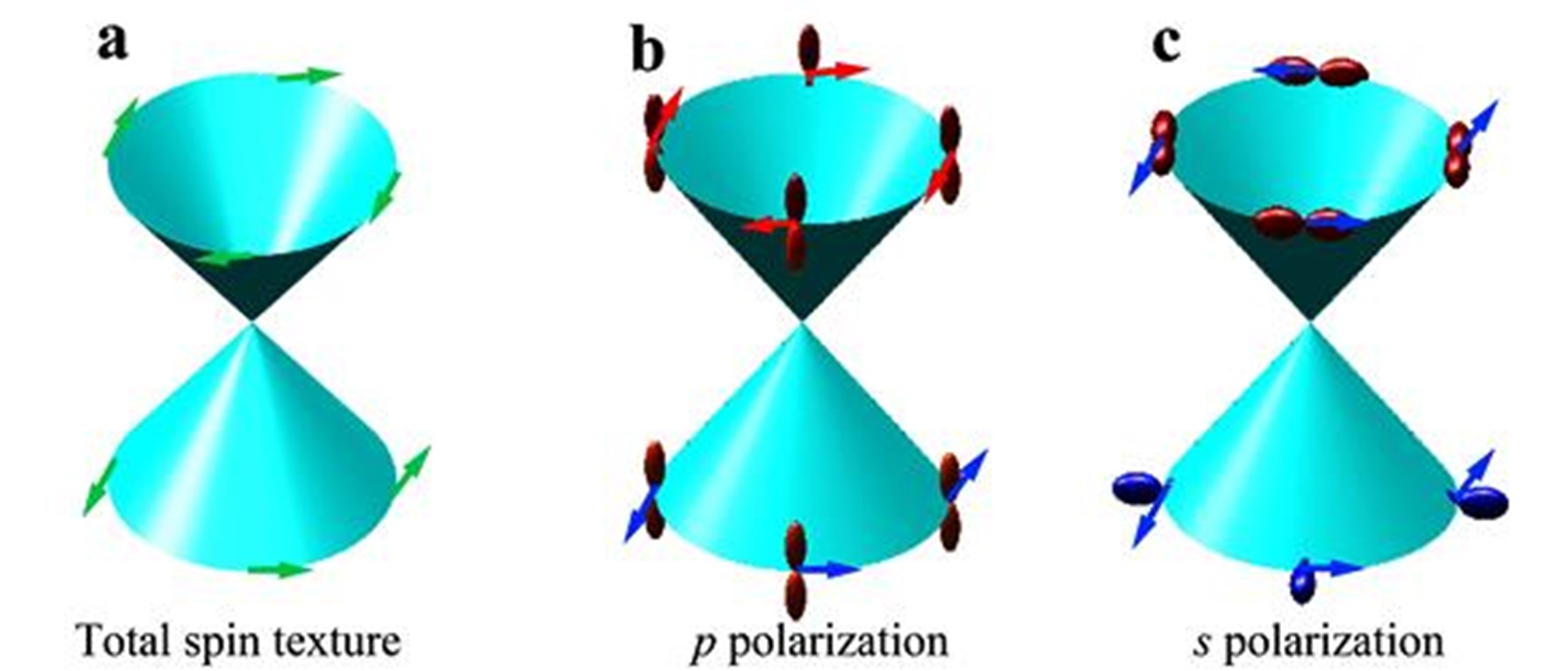
图四， 理论预言不同极化光测试时的spin-orbital texture

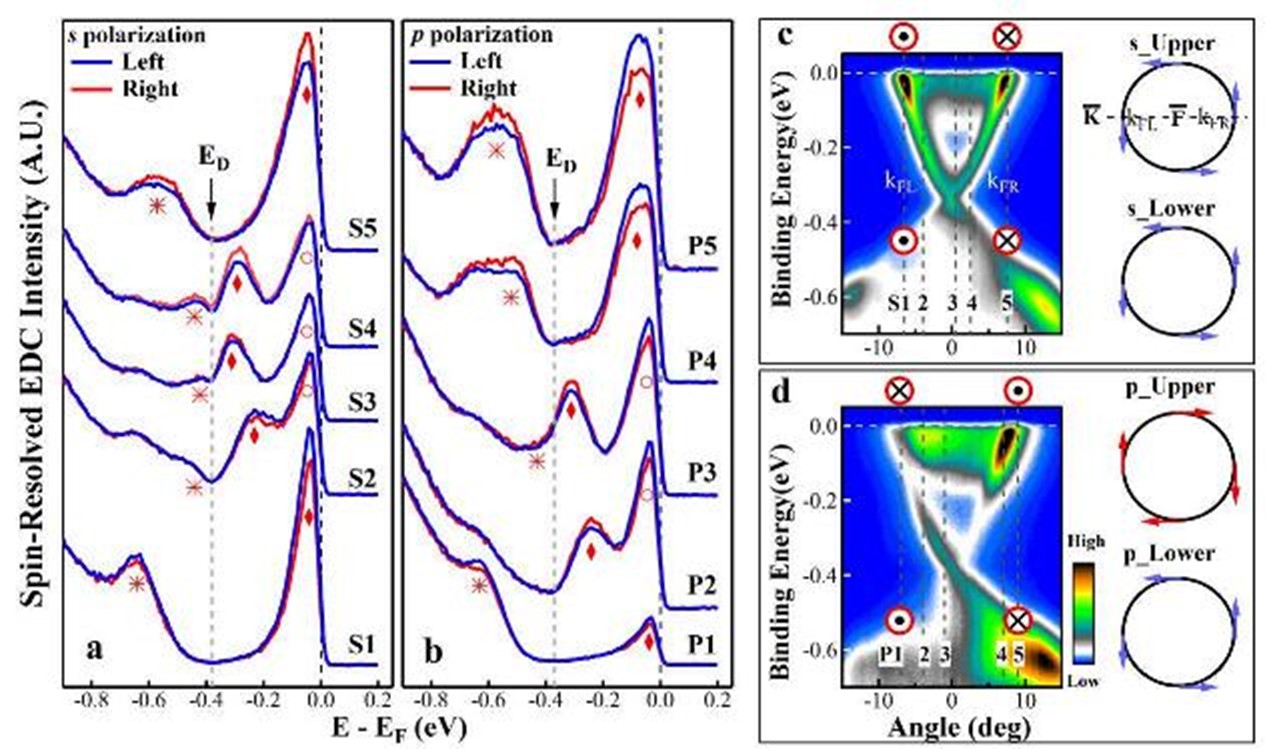
图五， 不同极化光下，SARPES的测试结果

　　2. 拓扑超导体 如前面所述，拓扑绝缘体是一种由强自旋耦合产生体带反带能隙，带隙中存在由时间反演对称性保护的无能隙边缘态或表面态的奇异量子物态，而拓扑绝缘体的发现，引发了超导体类比物态，拓扑超导体的研究热潮[26.27]，其拓扑非平庸的体能带会在超导能隙中导致马约拉纳束缚态(Majorana bound states)或马约拉纳费米子(Majorana fermions)的产生。 Majorana 费米子是其自身的反粒子，因其遵循非阿贝尔交换特性，在量子计算中拥有巨大的应用前景【28】。

　PbTaSe2单晶的空间群与SnTaS2 类似，拥有层状六角结构，但是由于晶体为非中心反演对称，会形成由镜面对称性保护的拓扑 Weyl 节线态以及靠近费米能级非平庸的表面态【29】。结合螺旋自旋极化的表面态以及超导电性，PbTaSe2 被认为是拓扑超导体的候选材料。 很快，与 PbTaSe2等电子结构的SnTaS2，因其 Tc~2.8 K 的超导电性以及靠近费米能级拓扑鼓状表面态而被列入拓扑超导的候选材料【30】

　我们利用角分辨光电子能谱实验手段，以及结合理论计算，对 SnTaS2 电子结构进行综合的研究。在实验发现 SnTaS2 存在两种电子结构的样品，新的样品拥有Sn和S两种截止面的特征能带，使得我们得到更完整的能带结构，其与理论计算结果更为相似。 同时在计算结果的辅助下，我们对测量得到的表面态进行 指认，从费米面，能带结构贡献更加深刻的解读了测量结果。通过自旋分辨的角分辨光电子能谱，我们对穿越费米能级的表面态 SS2 和 SS5 的自旋性质进行了研究。 在K-M-K方向观测到了类Rashba 结构的 SS5 表面态，我们在高对称M点和偏离的位置测量了自旋极化。在高对称M点没有明显的自旋极化特征，当测量位置在两支能带 SS5L 和 SS5R明显分离时，自旋 Y 和 Z 分量呈自旋极化，且二者极化方向相反【31】。

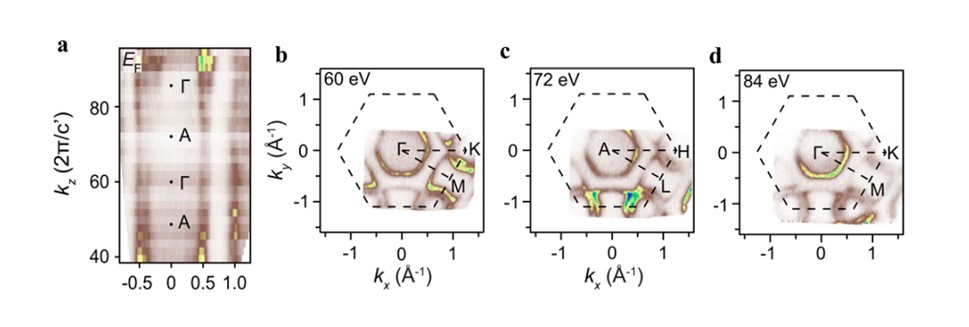
图六 SnTaS2 的 kz确定以及相应的费米面

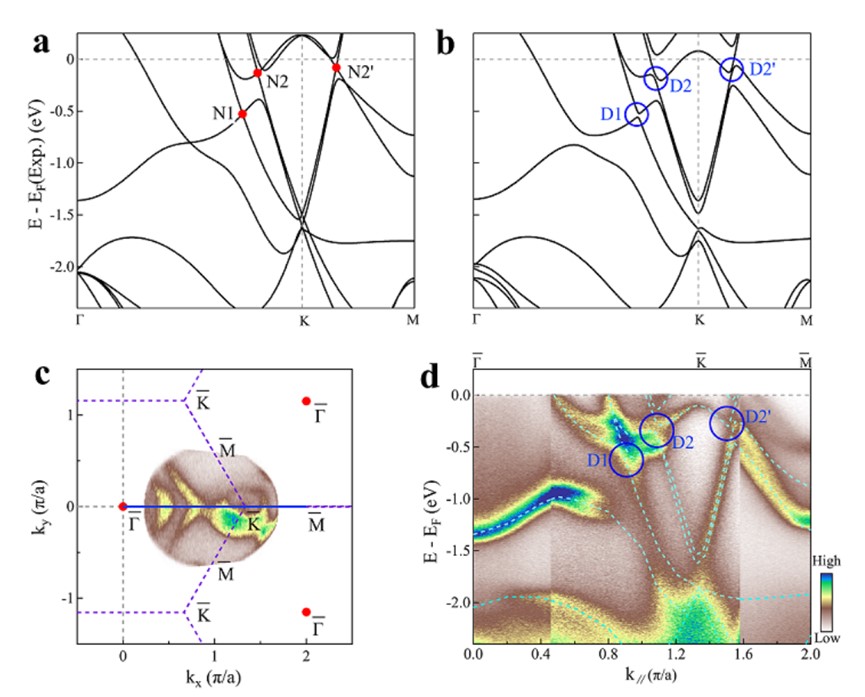
图七 SnTaS2 中 Dirac 节线态的确认

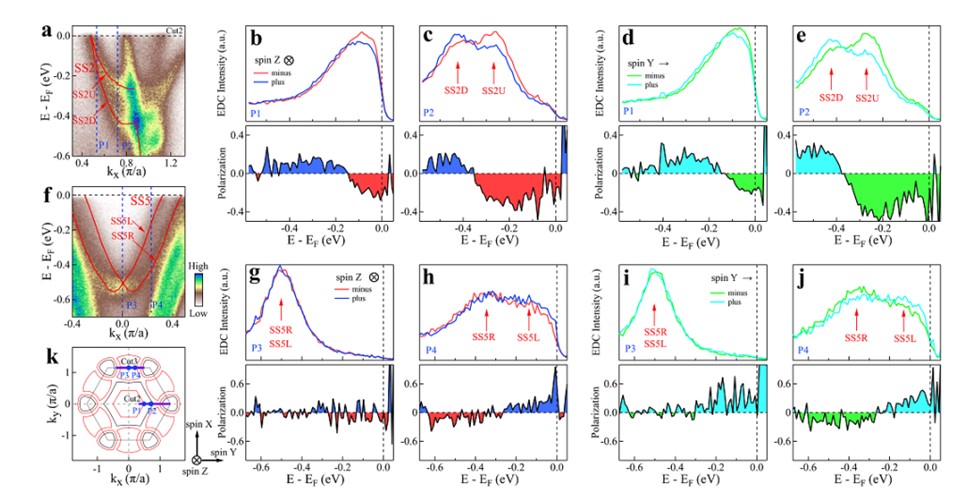
图八 表面态自旋极化

　　3. 拓扑半金属 在节点型拓扑半金属的研究中，已经有研究组将拓扑量子材料进一步拓展到节线态的半金属。与孤立节点型半金属不同，节线型半金属材料其Dirac或Weyl 线性交叉会在动量空间延伸成封闭的环或者一条线【32】。 与此同时，与 Weyl 半金属中一维费米弧表面态类似，节线态半金属中特征的表面态为二维拓扑鼓面态 (Drumhead Surface States)【33】，其最主要的特征是嵌入在节点环二维投影的体能带能隙中【34，35】，另外，鼓面态的色散很小，贡献很大的态密度【36】，也被认为可以实现高温超导，磁性以及其他关联效应【36，37】

　在节线态和节面态的研究中，自旋轨道耦合对节线和节面态的保持，还是具有很大的影响。而实现真正的节线态量子输运，进而利用节线态的特性就需要我们找到这样的平台，即寻找弱自旋轨道耦合，节线态的能量位置靠近费米能级且没有其他能带穿越费米能级的所谓真正的，干净的节线态材料。 近期，由轻元素构成的超导体 NaAlSi 被理论预言为拓扑节线态半金属，其简单的能带结构非常符合我们希望找到的真正的干净的节线态材料。

　利用可变光子能量的角分辨光电子能谱并结合理论计算，对 NaAlSi的电子结构进行了研究，并在其中观测到多种拓扑态【38】。 首先我们在 NaAlSi 中能量在费米能以下4 eV内观察到两组拓扑节面态，成为实验上第二个验证的节面态材料体系；另外我们发现了位于 kz = 0和π/c平面内两套同心节线环：这两个节线环并不相同，其内圈的节线环为 type-I 型，而外圈的节线环为 type-I型，同时在四个Γ-X方向嵌入了四个 type-III 型节点。由于 NaAlSi 中较弱的自旋轨道耦合，Dirac 点打开的能隙很小，使得 NaAlSi 接近于一个真正的节线态体系。 与此同时，NaAlSi 构成节线位置的能带非常靠近费米能级附近，且没有其他的平庸能带共存，因此，NaAlSi 成为一种干净的拓扑材料。 考虑到 NaAlSi 的超导性质以及多种拓扑物态，因此 NaAlSi 成为探索新奇的相和奇异性质的理想平台。

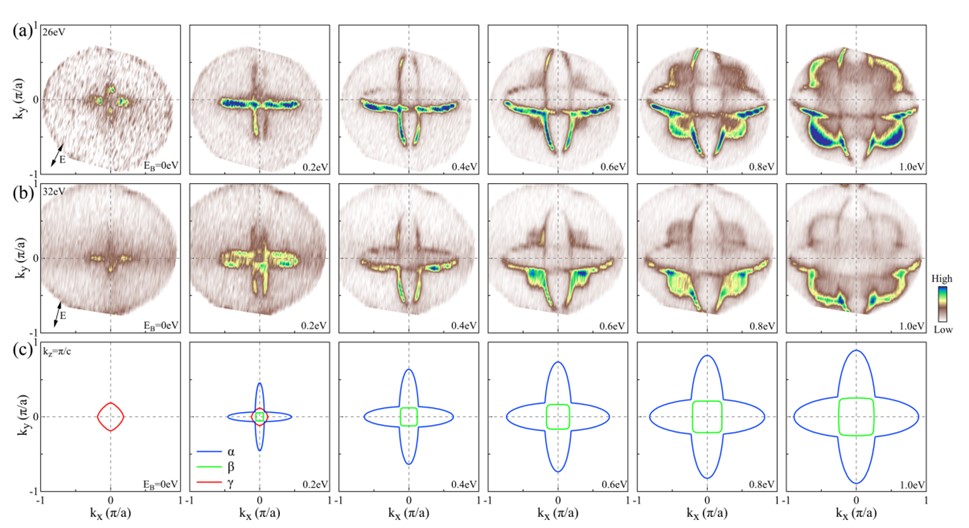
图九 NaAlSi等能面和理论计算的比较

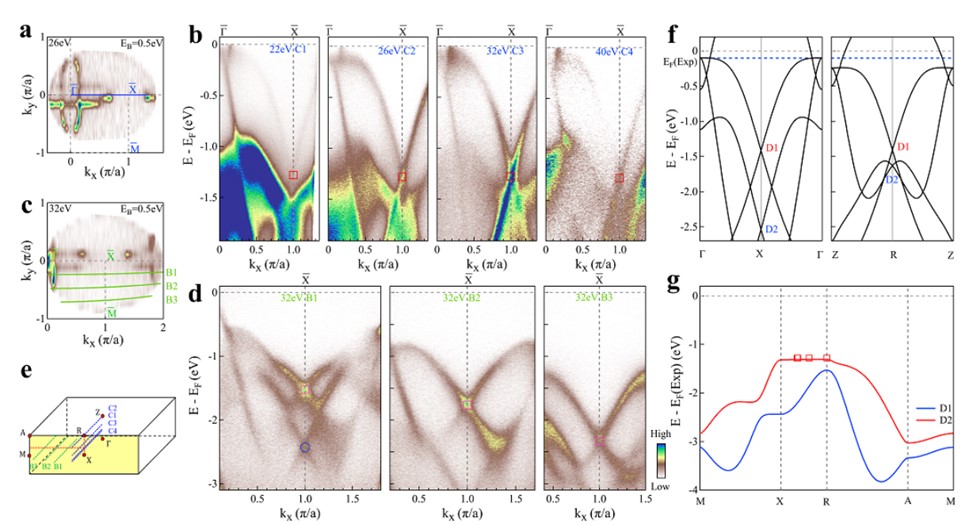
图十 NaAlSi中Dirac节面态的观测

　　4. 拓扑磁性材料 磁性拓扑材料是体内具有长程磁序的一类拓扑量子材料。与非磁性拓扑材 料类似，磁性拓扑材料也可以根据体态电子结构的拓扑性质分为磁性拓扑绝缘 体和磁性拓扑半金属等。其中，对于磁性拓扑半金属又可以根据体态能带交点 的简并度和它们在动量空间中形成的轨迹的维度而进一步分为磁性weyl半金属、磁性Dirac半金属和磁性nadal-line半金属【39】等。目前在理论上已经提出了大量的磁性拓扑材料，包括磁性拓扑绝缘体、磁性Weyl半金属、磁性Dirac半金属和磁性nodal-line半金属等。

　利用超高分辨的激光角分辨光电子能谱仪对EuCd2As2的电子结构进行测量。我们首次在EuCd2As2 中发现其电子结构在低温下存在明显的弛豫现象，并且弛豫时间可以长达2-3天之久【40】。此外，我们对在低温下完全弛豫的EuCd2As2样品进行变温实验，发现随着温度的增加 EuCd2As2 的电子结构发生显著的变化。 我们可以把整个变温过程划分成四个温度区间，其中在30K 以下温区EuCd2As2 的电子结构存在能带的劈裂和能带整体的移动，我们认为这种变化与其磁结构有关，但是在反铁磁转变温度附近（9.3K）EuCd2As2的电子结构并没有发生本质上的改变（能带数目没有变化且能量位置基本不变）。 对温度高于30K 的温度区间，EuCd2As2的能带在30K附近开始简并，并随温度的升高能带数目不再改变，而只是能量位置发生移动，这种变化与磁结构无关。以上的这些发现不能用EuCd2As2的表面重构和晶体结构的变化进行解释。到目前为止，我们还没找到一个合理的解释去理解以上的发现，该发现暗示在其背后可能存在新的物理机制。

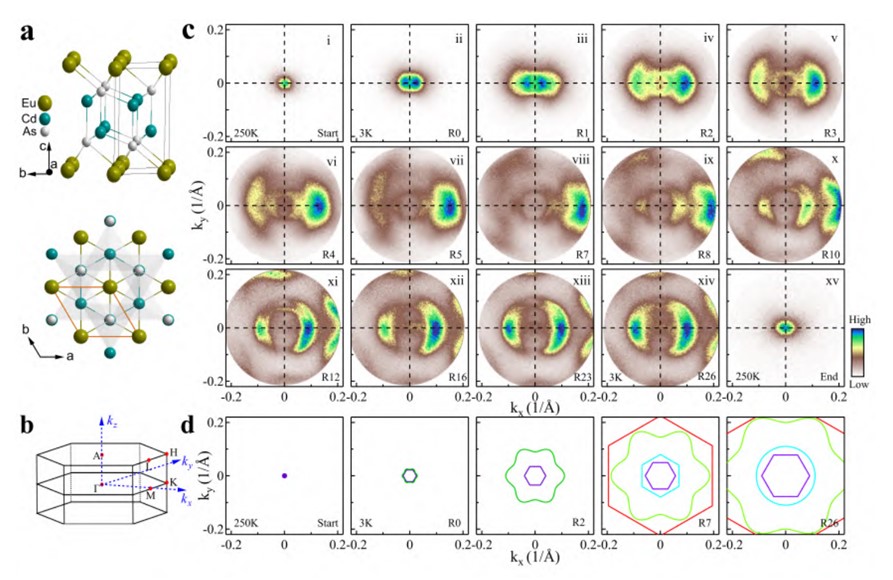
图十一 在 3 K 时测量EuCd2As2的费米面的弛豫

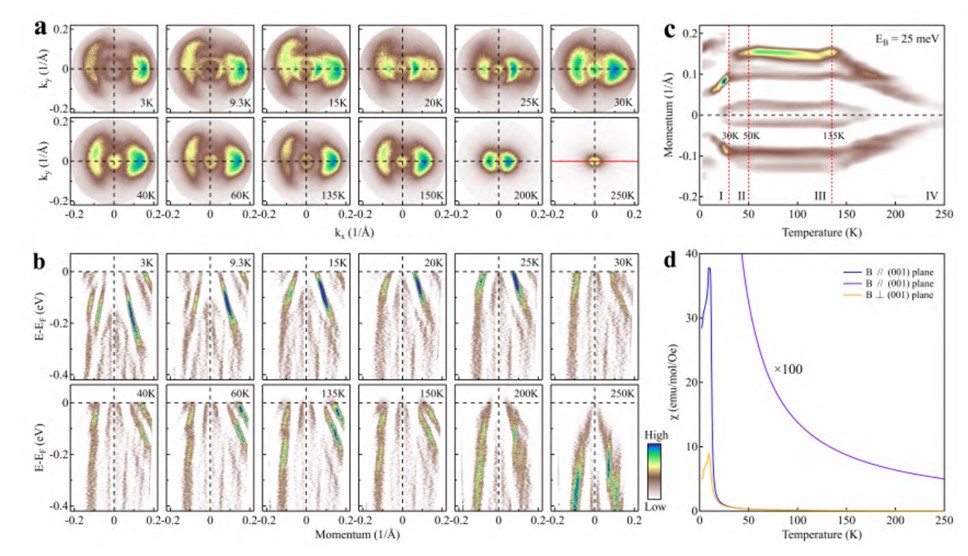
图十二 EuCd2As2温度依赖的电子结构

参考文献
1. K. v. Klitzing, G. Dorda, and M. Pepper, PHYSICAL REVIEW LETTERS 45, 494 (1980).
2. D. J. Thouless, M. Kohmoto, M. P. Nightingale, and M. den Nijs, PHYSICAL REVIEW LETTERS 49, 405 (1982).
3. M. Z. Hasan and C. L. Kane, Rev. Mod. Phys. 82, 3045 (2010).
4. X. L. Qi and S. C. Zhang, Rev. Mod. Phys. 83, 1057 (2011).
5. C. L. Kane and E. J. Mele, PHYSICAL REVIEW LETTERS 95, 226801 (2005).
6. B. A. Bernevig, T. L. Hughes, and S.-C. Zhang, Science 314, 1757 (2006).
7. L. Fu, C. L. Kane, and E. J. Mele, PHYSICAL REVIEW LETTERS 98, 106803 (2007).
8. L. Fu, PHYSICAL REVIEW LETTERS 106, 106802 (2011).
9. Z. K. Liu et al., Science 343, 864 (2014).
10. Z. K. Liu et al., Nature Materials 13, 677 (2014).
11. S. M. Young, S. Zaheer, J. C. Y. Teo, C. L. Kane, E. J. Mele, and A. M. Rappe, PHYSICAL REVIEW LETTERS 108, 140405 (2012).
12. H. Weng, C. Fang, Z. Fang, B. A. Bernevig, and X. Dai, PHYSICAL REVIEW X 5, 011029 (2015).
13. B. Q. Lv et al., Nature Physics 11, 724 (2015).
14. S.-Y. Xu et al., Science 349, 613 (2015).
15. Z. K. Liu et al., Nature Materials 15, 27 (2016).
16. X. Wan, A. M. Turner, A. Vishwanath, and S. Y. Savrasov, PHYSICAL REVIEW B 83, 205101 (2011).
17. A. A. Burkov, M. D. Hook, and L. Balents, PHYSICAL REVIEW B 84, 235126 (2011).
18. S. Zhu et al., Science 367, 189 (2020).
19. P. Zhang et al., Science 360, 182 (2018).
20. L. Fu and C. L. Kane, PHYSICAL REVIEW LETTERS 100, 096407 (2008).
21. Zhang, H. Topological insulators in Bi2Te3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438 (2009).
22. Chen, C. et al. Robustness of topological order and formation of quantum well states in topological insulators exposed to ambient environment. Proceedings of the National Academy of Sciences 109, 3694 (2012).
23. Guodong Liu, et al., Review of Scientific Instruments 79 (2008) 023105.
24. Chen, C.Y. et al. Tunable Dirac Fermion Dynamics in Topological Insulators. Sci. Rep. 3, 2411
25. Zhuojin Xie, et al. "Orbital-Selective Spin Texture and its Manipulation in a Topological Insulator" Nature Communications 5, 3382(2014)
26.Qi X L, Zhang S C. Topological insulators and superconductors [J]. Reviews of Modern Physics,83(4) 2011.
27.Sato M, Ando Y. Topological superconductors: a review [J]. Reports on Progress in Physics, 80(7),2017.
28.Alicea J. New directions in the pursuit of Majorana fermions in solid state systems [J]. Reports on Progress in Physics, 2012, 75(7):
29.Bian G, Chang T R, Sankar R, et al. Topological nodal-line fermions in spin-orbit metal PbTaSe2 [J]. Nature Communications, 2016, 7(1): 10556.
30.Chen W, Liu L, Yang W, et al. Evidence of topological nodal lines and surface states in the centrosymmetric superconductor SnTaS2 [J]. Physical Review B, 2021, 103(3): 035133
31.Chunyao Song,et al. Observation of spin-polarized surface states in the nodal-line semimetal SnTaS2, Physical Review B 107, 045142 （2023）
32.Bzdušek T, Wu Q, Rüegg A, et al. Nodal-chain metals [J]. Nature, 2016, 538(7623): 75-78.
33.Weng H, Liang Y, Xu Q, et al. Topological node-line semimetal in three-dimensional graphene networks [J]. Physical Review B, 2015, 92(4): 045108.
34.Burkov A A, Hook M D, Balents L. Topological nodal semimetals [J]. Physical Review B, 2011, 84(23): 235126
35.Heikkilä T T, Kopnin N B, Volovik G E. Flat bands in topological media [J]. JETP Letters, 2011, 94(3): 233
36.Kopnin N B, Heikkilä T T, Volovik G E. High-temperature surface superconductivity in topological flat-band systems [J]. Physical Review B, 2011, 83(22): 220503.
37.Huh Y, Moon E G, Kim Y B. Long-range Coulomb interaction in nodal-ring semimetals [J]. Physical Review B, 2016, 93(3): 035138.
38.Chunyao Song, et al. Spectroscopic evidence for Dirac nodal surfaces and nodal rings in the superconductor NaAlSi , Physical Review B 105, L161104 (2022)
39.Burkov A A, Hook M D,et al., Topological nodal semimetals[J]. Physical Review B, 84, 235126(2011)
40. Yang Wang, Cong Li, et al, Giant and reversible electronic structure evolution in a magnetic topological material EuCd2As2 ,  Physical Review B 106, 085134 (2022)